Расчет размерных цепей. Колчков В.И.

Главная Форум Теория Практикум Задания Информация Контакты

УЧЕБНИК "МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ"

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (МАМИ)
УНИВЕРСИТЕТ МАШИНОСТРОЕНИЯ
________________________________________________
Кафедра «Стандартизация, метрология и сертификация»

РАСЧЕТ РАЗМЕРНЫХ ЦЕПЕЙ

Методические указания

Москва 2012

В.И. Колчков
УДК: 389

Размерные цепи отражают объективные размерные связи в конструкции машины при сборке, а также размерные связи в технологических процессах обработки или измерения деталей.

Размерные цепи позволяют составить метрическую модель изделия и оптимизировать требования к точности геометрических параметров, с целью обеспечения показателей качества функционирования в заданных пределах при установленных затратах на производство.

Размерная цепь - совокупность взаимосвязанных размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи.

В общем случае размерная цепь может быть представлена в виде зависимости параметров , , . . . , , влияющих на параметр Y.

Метрическая модель описывается уравнением:

Y= F (, ,…,). (1)

Уравнение, связывающее отклонения размеров в размерной цепи:

(2)

Размерная цепь состоит из составляющих и замыкающего размеров.

Замыкающим называется размер, получающийся последним в результате обработки или сборки изделия. Замыкающий размер получается как результат действий, связанных с обработкой или сборкой изделий.

Составляющими называют все остальные размеры. Составляющие размеры получаются в процессе обработки деталей.

На рис.1 показана деталь, размеры которой получены в процессе обработки в одной из следующих последовательностей: ,, или . Для любой из указанных последовательностей обработки размерная цепь будет состоять из четырёх (m = 4) размеров (рис.1b). Размеры , являются независимыми и поэтому называются составляющими.

Размер специально не изготовляется и не контролируется в процессе обработки детали, а получается результирующим после того, как с заданной точностью будут выполнены размеры ,. Такой размер является замыкающим.

При обозначении составляющих размеров замыкающий размер обозначается . В сборочной размерной цепи замыкающий размер – это всегда размер между осями или поверхностями разных деталей (зазор, натяг, отклонение от соосности и т.п.).

По отношению к замыкающему все составляющие размеры делятся на увеличивающие и уменьшающие. Увеличивающим называют размер, с увеличением которого замыкающий размер увеличивается (т.е. для которого >0). Уменьшающим называется размер, с увеличением которого замыкающий размер уменьшается (т.е. передаточная функция отрицательна <0 ).

Размерные цепи, для которых = +1, называют линейными. К нелинейным относят плоские и пространственные цепи с произвольно направленными размерами.

Для обозначения размеров обычно применяют прописные буквы латинского алфавита: , или любые другие.

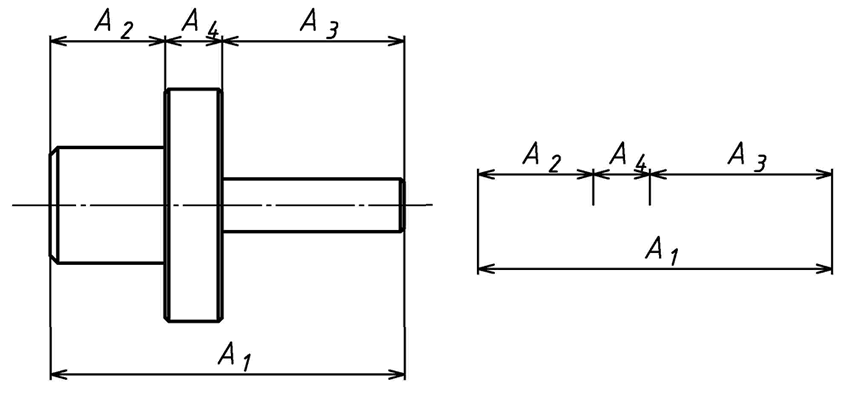
Пример размерной цепи

Рис1

При расчёте размерных цепей применяются следующие условные обозначения:

- номинальный размер любого составляющего размера;

- замыкающий размер;

Т, Т- допуски составляющего и замыкающего размеров;

Е – обозначение отклонения;

- верхнее отклонение, например ;

- нижнее отклонение, например .

В размерных цепях применяют отличные от системных обозначений( в которой, как известно, ES, EI – отклонения отверстий; es, ei – отклонения валов), так как многие размеры размерных цепей не подходят под понятия “отверстие” или “вал”.

- среднее отклонение, определяющее середину поля допуска, например .

- наибольший, наименьший предельные и средний размеры составляющего звена;

- наибольший, наименьший предельные и средний размеры замыкающего размера.

- передаточное отношение (или передаточная функция j – го размера.

РАСЧЁТ РАЗМЕРНЫХ ЦЕПЕЙ

Метод max-min

Для линейной размерной цепи уравнение (1) может быть записано в следующем виде:

, (3)

где n- число увеличивающих, p- число уменьшающих звеньев, причём n+p=m-1.

В общем случае . (4)

На схемах увеличивающие звенья можно отмечать стрелкой, направленной вправо ( ), уменьшающие - влево () (рис.1).

Предельные размеры рассчитываются по следующим формулам:

(5)

(6)

В большинстве случаев удобнее пользоваться расчётом предельных отклонений:

(7)

, (8)

затем среднее отклонение замыкающего размера

(10)

Формула (10) может быть получена в результате сложения и деления на уравнения (7) и (8).

В общем случае (11)

Если вычесть из уравнения (5) уравнение (6), получим основное уравнение связи допусков составляющих размеров с допуском замыкающего размера при полной взаимозаменяемости, т.е. при допущении, что возможно сочетание всех наибольших увеличивающих размеров с наименьшими уменьшающими и наоборот:

(12)

Допуск замыкающего размера равен сумме допусков составляющих размеров.

Из этого следует, что:

а) исходные размеры (к которым предъявляются функциональные требования, от точности которых зависит качество изделия) не следует делать замыкающими при указании исполнительных размеров на чертеже;

б) если это невозможно, то необходимо выполнить принцип кратчайшей размерной цепи, т.е. исходный размер делать зависимым от минимального числа составляющих размероПри условии обеспечения полной взаимозаменяемости её решают в такой последовательности:

1)определить допуск замыкающего размера по формуле (12);

2)определить и по формулам (7) и (8);

3)проверить расчёт по формуле:

(15)

Метод регулирования

Этот метод основан на применении регулятора, компенсирующего значительные отклонения замыкающего размера от заданных значений.

Компенсатором может быть специальная деталь, например набор прокладок или устройство ( винт или гайка, клин и т.п. ). В некоторых случаях предусматривают технологический компенсатор - избыток материала на одной из деталей, который удаляется при сборке пригонкой замыкающего размера до заданных пределов.

Номинальный размер компенсатора определяется из уравнения

. (24)

Знак “+” соответствует случаю, когда компенсатор является увеличивающим звеном, знак “-“ - когда компенсатор – уменьшающее звено.

Диапазон регулирования компенсатора определяется из уравнения

. (25)

Расчёт увеличивающего компенсатора проводиться по следующим формулам:

. (26)

Предельные отклонения компенсатора от номинального значения определяются по уравнениям

; . (27)

или по предельным отклонениям составляющих звеньев

. (28)

Предельные размеры компенсатора могут быть определены по следующим формулам:

(29)

или только для увеличивающего компенсатора – из уравнений

. (30)

Расчёт уменьшающего компенсатора проводится по формулам

. (31)

Предельные отклонения компенсатора определяются по (27), или по предельным отклонениям составляющих звеньев:

. (32)

Предельные размеры уменьшающего компенсатора можно определить по формулам (29) или из следующих уравнений:

. (33)

Пример

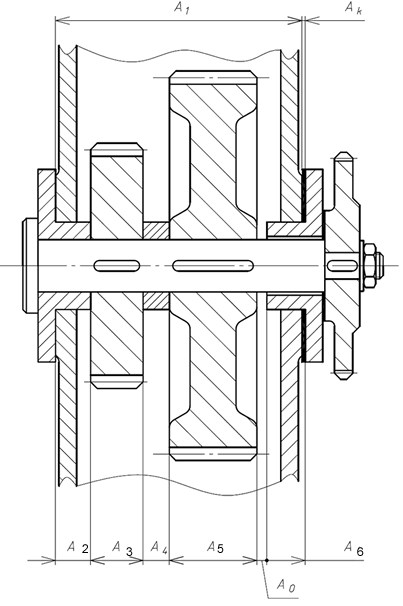
Изделие с компенсаторами - прокладками

Рис 3

На рис.3 изображена часть редуктора, детали которого образуют размерную цепь из осевых размеров. Для нормального функционирования редуктора необходим осевой зазор в пределах 1-1,5 мм. Оптимальная точность осевых размеров по 10-му квалитету. Заданы номинальные размеры, составляющие размерную цепь:

мм, мм, мм, мм, мм, мм, мм.

Для регулирования осевого зазора предусмотрен компенсатор в виде прокладок. Рассчитать предельные значения компенсатора, а также толщину и максимальное количество прокладок, необходимое для одного изделия.

Решение:

Замыкающий размер может быть расположен в любом месте между деталями 2, 3, 4, 5, 6. На рис.3 он изображён между размерами и . Анализ составляющих размеров показывает что, - увеличивающий размер, и - уменьшающие, компенсатор - увеличивающий.