Главная Форум Теория Практикум Задания Информация Контакты
УЧЕБНИК "МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ"
Колчков В.И. МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ. М.:Учебное пособие
3. Метрология и технические измерения
3.9.5. Примеры обработки результатов измерений
Если совокупность случайных величин, подчиняется закону нормального распределения или закону близкому к нормальному, то применяя соответствующие критерии, можно установить, что рассматриваемое эмпирическое распределение наилучшим образом соответствует именно этому закону.
При контроле партии деталей по какому-либо размеру или при многократном измерении одной детали по какому-либо размеру мы встречаемся со случаем, когда результаты наблюдений представляют собой совокупность значений дискретной случайной величины, т. е. совокупность действительных значений размера или значений погрешностей размера.
Рассмотрим примеры обработки результатов наблюдений.
Методику статистической обработки результатов наблюдений рассмотрим на примере измерения дискретных размеров валов 
12 h10 (-0,07), обработанных на токарном станке. Размер выборки из генеральной совокупности (объём всей партии) примем равным N = 200. Измерения проводим на приборах типа длиномер или оптиметр с ценой деления 0,001 мм.
Анализируя результаты наблюдений, приходим к выводу, что среди них встречаются значения существенно отличающееся от большинства результатов, они являются промахами или грубыми ошибками. Такие наблюдения, могут быть вызваны невнимательностью контролера, попаданием в выборку посторонних деталей, а также другими причинами, нарушающими нормальные условия получения опытных данных. Следует иметь в виду, что эти наблюдения визуально резко отличаются от среднего результата для данной выборки. При наличии промахов причины их должны быть проанализированы и устранены.
* Наблюдение, которое является промахом, исключают из совокупности, а остающиеся наблюдения снова обрабатывают и получают новые значения, 
и s, после чего проводят дальнейший анализ результатов и исключают при необходимости другие промахи, пользуясь критериями Колмогорова, Ирвина или другими.
При предварительных расчетах исключают погрешности, т.е.отклонения от , превосходящие по абсолютной величине З
.
Полученные после предварительного анализа результаты наблюдения располагаем в возрастающем порядке, тем самым образуем вариационный ряд. Находим из всего числа наблюдений максимальное и минимальное значения dmax и dmin, находим размах.
В нашем примере минимальное значение наблюдаемого размера равно 11,915 мм, а максимальное равно 12,005 мм, тогда размах R, равный разности полученных предельных значений, равен: R = dmax - dmin = 12,005 - 11,915 = 0.09 мм.
Далее вариационный ряд разбиваем на k интервалов. Число интервалов k в определённой степени зависит от объёма выборки N и может быть принято по следующим рекомендациям: 5 < k < 7, при N < 40; 7 < k < 9, при 40 < N < 100; 9 < k < 12, при 100 < N < 500, кроме того при небольшом числе интервалов удобным выбирать нечётное k. Из представленных рекомендаций видно, что значения существенно перекрываются и выбор числа интервалов не является определяющим, таким образом рекомендации носят ориентировочный характер.
Примем k = 9, тогда величина интервала равна R/k = 0,09/9 = 0,01 мм, а половина интервала равна 0,5R/k = 0,005 мм. Находим значения середин интервалов и образуем интервальный ряд, для чего к dmin прибавим значение 0,5R/k, к полученному значению прибавим снова 0,5R/k и так далее, получим в итоге dmax - 0,5R/k, т.е. 12,000 мм.
Далее находим количество наблюдений попавших в каждый из интервалов, например, в интервал 11,935 
11,945 попало 20 результатов; в интервал 11,975 11,985 попало 12 результатов наблюдений и т.д. Следует иметь в виду, что значения, попавшие на границу интервала, включают в левый интервал.
Число наблюдений, попавших в данный интервал, называют частотой.
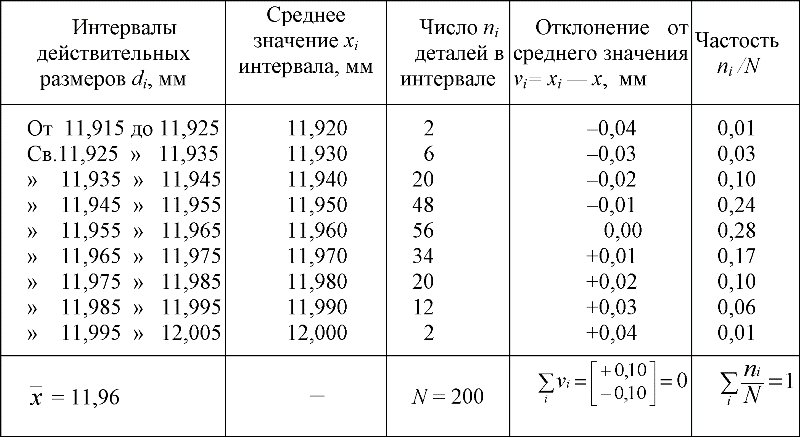
Порядок обработки результатов и пример оформления расчётов приведён в таблице 3.4. Значения и s определяются по формулам 3.11 и 3.12.
= (11,920 • 2 + 11,930 • 6 + … + 12,000 • 2) / 200 = 11,960 мм
мм
Таблица 3.4. Пример обработки результатов измерения
Характер рассеяния значений случайной величины, которой в рассматриваемом примере является действительный размер вала, более наглядно определяется гистограммой, состоящей из прямоугольников, высота которых равна частоте, а основание величине интервала.
Рассеяние определяется также эмпирической кривой распределения, которую называют полигоном распределения (рис. 3.5). Графическое представление результатов при ручной обработке удобно выполнять на миллиметровой бумаге. По оси абсцисс откладывают интервалы действительных размеров валов, а по оси ординат - высоты прямоугольников равные частотам.
Расстояния по оси абсцисс и по оси ординат для лучшей наглядности рекомендуется откладывать в отношении равном 0,8 1,0. На рис. 3.5 представлены полигон и гистограмма распределения размеров валов, также расположение поля допуска отражающего требования к точности по чертежу, как можно видеть эмпирические результаты несколько не совпадают с требованиями технической документации, что в принципе так и должно быть.
Например, несовпадение координаты середины поля допуска с эмпирическим центром группирования равно 0,005 мм, а размах превышает допуск на величину равную 0,09 0,07 = 0,02 мм.
Для заключения о годности партии необходимо провести анализ полученных результатов по следующим признакам:
- соответствие эмпирического распределения закону нормального распределения;
- оценка доверительных вероятностей эмпирических параметров;
- установление технологических допусков.
Рис. 3.5. Гистограмма и полигон распределения случайной величины
Анализ результатов измерения случайных величин становиться возможным, если знать, какому теоретическому закону распределения вероятностей случайной величины соответствует эмпирическое распределение.
Исходя из формы эмпирической кривой, и из значений эмпирических параметров выдвигается гипотеза о соответствии ее тому или иному теоретическому закону распределения.
Следует иметь в виду важность графического представления формы эмпирической кривой, на которую влияют, кроме всего прочего, выбор числа интервалов и соотношение значений по осям абсцисс и ординат.
Соответствие эмпирического распределения предполагаемому теоретическому распределению устанавливается на основании критериев 
по ГОСТ 11.006-74, например критерия Колмогорова.
Сравнение характеристик эмпирического и теоретического распределений проводят следующим образом. Рассматривают значения параметров эмпирического и принятого теоретического распределений. Параметры и s, определённые по данным выборки, дают лишь приближенную характеристику точности генеральной совокупности исследуемых объектов.
Характеристикой рассеяния значений случайной величины в генеральной совокупности служат математическое ожидание MX и среднее квадратическое отклонение .
Между вероятностными характеристиками MX и и эмпирическими значениями и s различия заключаются в том, что первые рассматриваются как постоянные неизвестные величины, характеризующие распределение генеральной совокупности, а вторые, являются случайными величинами, определенными из выборочной совокупности и дают лишь приближенную оценку MX и .
C увеличением объема выборки и числа наблюдений, разница между MX и , а также между и s уменьшается.
Обработка результатов наблюдений выборки заданного объема, позволяет установить границы, внутри которых с определенной, вероятностью, будут находиться значения параметров генеральной совокупности.
Степень этого доверия или так называемый доверительный интервал выбирают исходя из технических требований на показатели качества функционирования изделия.
Границы доверительного интервала определяют доверительную вероятность, которая характеризует надёжность принятого результата.
Для нормального распределения таким доверительным интервалом, например, для математического ожидания MX будет интервал, имеющий границы MX равные ±3
, где - среднее квадратическое отклонение для распределения величин 
.
Так как 
, то границами доверительного интервала будут 
.
Из таблицы значений Ф0 (z) находим, что в границах ± z1= ± 3 лежит 99,73% всех значений случайной величины X, выраженной через z, так как 2Ф0 (3) = 2 • 0,49865 = 0,9973. Таким образом, с надежностью 0,9973 можно утверждать, что значение MX лежит в интервале X ± 3 .
Так как x и s - случайные величины, то доверительные интервалы, как это следует из приведенного выше расчета, зависят от множителя, при , который обозначим для общего случая через z.
Очевидно, надежность того, что значение MX лежит в пределах X ± z , будет больше, чем 0,9973, если z > 3, и меньше, чем 0,9973, при z < 3.
Обычно задаются надежностью, равной одной из следующих величин: 0,90; 0,95; 0,99; 0,999, что соответствует значениям z, равным 1,645; 1,96; 2,576 и 3,291.
Рассмотрим пример, примем, что рассмотренное выше распределение погрешностей изготовления валов являющееся выборкой объёмом N = 200 имеет нормальное распределение, тогда:
.
Доверительный интервал для MX определяют по формуле:
- z < MX < +z
Тогда с надёжностью 0,9 или 90% можно ожидать, что:
11,96 - 1,645 • 0,001 < MX < 11,96 + 1,645 • 0,001 или 11,958 < MX < 11,962.
Для выборок, малых объемом, множитель z должен быть заменён множителем 
, который находят по таблице 3.5 по распределению Стьюдента.
Значение зависит от объема выборки, т. е. от N - 1 пользуясь этими таблицами, можно получить, например, что при N = 20 и надежности 0,9 коэффициент = 1,73; при том же значении N и надежности 0,95; 0,99 и 0,999 величина будет равна соответственно 2,09; 2,86; 3,88.
Выбор надёжности определяется объектом производства, например: для изделий общего назначения можно принять надёжность 0,9; для изделий повышенной надёжности - 0,95; для авиационной техники - 0,99; наконец - 0,999 или как говорят: "три девятки" для особо ответственных изделий, нарушение работоспособности которых представляет собой опасность для жизнедеятельности людей.
Таким образом, если бы значения = 11,96 и s = 0,015 были получены из выборки объемом 20 шт., а не 200 шт., как это было показано в предыдущем примере, то при заданной надежности 0,9 границы доверительного интервала были бы следующими:
11,96 - 1,73 • 0,003 < MX < 11,96 + 1,73 • 0,003 или 11,955 < MX < 11,965.
При надежности "три девятки" получили доверительный интервал значительно больший 11,96 - 3,88 • 0,003 < МХ < 11,96 + 3,88 • 0,003 или 11,948 < МХ < 11,972.
Таблица 3.5. Значение коэффициента Стьюдента при разной доверительной вероятности Р
При уменьшении объема выборки и увеличении требуемой надежности величина доверительного интервала будет возрастать, т. е. границы возможных значений величины MX будут расширяться.
Аналогично могут быть определены доверительные интервалы для значения .